New Page 1

Contemporary greenhouse operations require precise control of irrigation and nutrient supply in order to optimize crop growth and minimize cost and pollution due to effluents. Moreover in Mediterranean countries there is a need to minimize water waste due to seasonal shortages. In modern greenhouses nutrient supply is computer controlled and based on measuring salinity and compensating deficiencies by a mix of clean water and two stock nutrient solutions. The process of applying this solution to the crop presents several control problems such as time delays and seasonal variations due to plant growth. Several proposals to the nutrient supply problem have been proposed such as direct feedback control of drain water flow in both closed and open growing systems using flow measurement of the drain water. On the other hand progress has been achieved in model prediction of crop irrigation needs. Usually a transpiration model is used that predicts plant transpiration based on ambient conditions (temperature, solar radiation, CO₂ concentration and vapor saturation deficit). This approach leads to open loop control of water and nutrient supply based on model estimation of plant needs.

This method proposes an intermediate approach where a crop transpiration model of convenient form is used to predict the necessary supply of water. At the same time drain water flow from the crop is measured using an appropriate device. Using the error between drain measurement and model estimate the coefficients of the model are iteratively adapted. The adaptation process is continuous so that the model accounts for seasonal variation of crop growth.

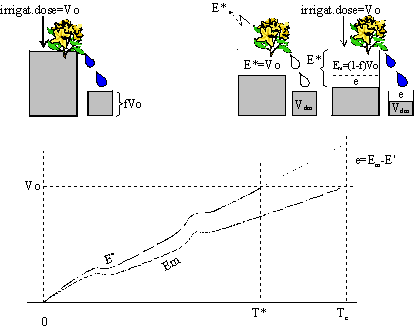
In common greenhouse-growing practice the irrigation water is supplied in specified time cycles. In each cycle the amount of water supplied, (designated V_o), is determined by the grower manually in order to satisfy crop requirements. The approach taken is to ensure that the growing medium saturates by the presence of an amount of drain water. The desired drain is typically around 20% of the irrigation amount (V_o), required to secure desired nutrients concentration in the root environment. If we define the fraction of drain water as f, and the true crop requirement, which is the amount of real crop evapotranspiration, as E^*, then the current growing practice is expressed by

Assume that a model exists relating crop transpiration to climate conditions, of the form

Where crop transpiration E (kg/m²/s) is related to solar radiation S(W/m2), humidity deficit (1-RH) and ambient air temperature T (^oC), through suitable coefficients (α,β,γ), then crop transpiration E* could be calculated by integrating this model for the duration of the irrigation cycle. However in the general case the model of Eq.2 has unknown parameters dependent on factors such as crop type, growth stage (LAI) etc.

However if a measurement of the drain water is available then the true crop transpiration can be determined by integrating drain water rate and using the equation

The concept of model prediction of irrigation needs and its error appearance in measured drain

The alternative proposed here is to utilize this measurement in order to determine the unknown parameters of Eq.2. Then with well tuned parameters the irrigation process could be controlled in a feed-forward loop. Parameter tuning can be accomplished using a minimization algorithm if an appropriate performance function is devised. In this case the performance criterion to minimize is simple to create. During the irrigation cycle the integral of Eq.2 is monitored so that the estimated evapotranspiration (E_m) is available

The proposed method is based on common measurements of ambient dry-bulb temperature, relative humidity and crop level solar radiation which are used as a means for controlling the greenhouse environment. The method additionally requires the existence of a flow sensor (such as a tipping bucket) on the drainage of the irrigation channel.

Irrigation Optimization algorithm
1.	Define Vo, f
2.	Select initial parameters α,β,γ
3.	Apply Vo
4.	Do Loop
	Calculate Em (from Eq. 4)
	Measure drain and integrate Vdm
	While Em < (1-f) Vo
5.	Compute E* (from Eq.3)
6.	Compute J (from Eq.6)
7.	Call OPTIMIZER to update [α,β,γ] using J
8.	GoTo step 3


The Tipping Bucket installed at Kolovos greenhouse	View of the rose cultivation crop in perlite at Kolovos greenhouse

Irrigation Optimization algorithm